Proyecto Minimax-Scout (Código C++)

INTRODUCCIÓN

La teoría de juegos plantea que debe haber una forma racional de jugar a cualquier «juego» (o de negociar en un conflicto), especialmente en el caso de haber muchas situaciones engañosas y segundas intenciones; así, por ejemplo, la anticipación mutua de las intenciones del contrario, que sucede en juegos como el ajedrez o el póquer, da lugar a cadenas de razonamiento teóricamente infinitas, las cuales pueden también trasladarse al ámbito de resolución de conflictos reales y complejos. En síntesis, y tal como se comentó, los individuos, al interactuar en un conflicto, obtendrán resultados que de algún modo son totalmente dependientes de tal interacción.

Análisis

Para el siguiente proyecto utilizaremos dos tipos de algoritmos por un lado Minimax y por el otro el algoritmo de Scout los cuales nos brindaran las mejores soluciones.

El algoritmo de minimax consiste en la elección del mejor movimiento para el computador, suponiendo que el contrincante escogerá uno que lo pueda perjudicar, para escoger la mejor opción este algoritmo realiza un árbol de búsqueda con todos los posibles movimientos, luego recorre todo el árbol de soluciones del juego a partir de un estado dado, es decir, según las casillas que ya han sido rellenadas. Por tanto, minimax se ejecutará cada vez que le toque mover a la Inteligencia Artificial.

El algoritmo de Scout utiliza dos funciones con las cuales nos permitirá comprobar de forma rápida desigualdades evitándonos un alto desgaste computacional, este algoritmo no explora ramas que no lleven a una mejor solución  utilizando menos memoria al compararlos con otros como sss*.

Este algoritmo utiliza dos funciones principales TEST y EVAL, la primera función se encarga de resolver la desigualdad tiene tres entradas que son el Nodo N, el Valor v y el Operador que será > o =, y como salida nos devolverá un booleano indicando si se cumple o no la desigualdad.

La segunda función calculara el valor minimax de un nodo usando a TEST para calcular cuando deberá explorar o no una rama determinada su único parámetro de entrada será el Nodo a evaluar y su salida será el valor mínimo de dicho nodo. 

Diseño

Tenemos un tablero con 9 posiciones

En nuestro tablero ganara aquel que logre ubicar 3 símbolos seguidos ya sea en una fila, columna o diagonal, por otro lado empataremos si ninguno de los dos jugadores logra completar los tres símbolos seguidos. 

Empate = 0 ganador 1 = 1 ganador 2= -1

En nuestro tablero tendremos 9 grados de profundidad pero por cada grado habrá 9 nodos diferentes por las posiciones teniendo así 362880 posibilidades.

Implementación

Al ya saber cómo es el funcionamiento del juego entramos en la parte de la implementación del juego con los dos algoritmos antes mencionados (Minimax y Scout).

En la imagen anterior podemos observar las funciones que nos permiten obtener los valores máximos y mínimos de nuestro árbol. En nuestro caso utilizaremos en siguiente algoritmo que es el mismo pero en una sola función y recursivo. 

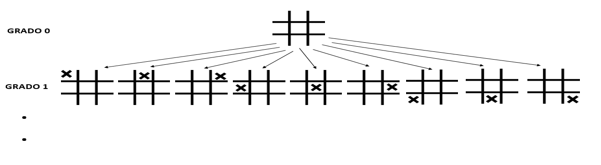
Al implementar nuestro algoritmo en el juego tic tac toe obtendremos algo parecido al siguiente árbol del juego en el que ya nos quedan tres niveles para concluir el juego.

Como podemos observar en la imagen anterior lo que el algoritmo busca es obtener los puntos máximos en el cual la maquina queda ganadora o el punto mínimo en el que la maquina empata analizando cada posible jugada que pueda hacer el adversario logrando sacar ventaja al anticiparse a los diferentes tipos de movimientos.

Ahora lo que haremos es implementar las dos funciones que contiene el algoritmo de Scout para comprobar las desigualdades y evitar explorar las ramas que no nos lleven a una mejor solución.

La parte del TEST nos sirve para verificar la desigualdad el cual nos arrojara un valor verdadero o falso

Mientras que el EVAL es la que decide si explorar el Nodo o no obteniendo el valor mínimo del NODO.

Codigo C++

#include <stdio.h>
char estado(int i) {
    switch(i) {
        case -1:
            return 'X';
        case 0:
            return ' ';
        case 1:
            return 'O';
    }
}
// determina si un jugador ha ganado, devuelve 0 de lo contrario.
void dibujo(int b[9]) {
    printf(" %c | %c | %c\n",estado(b[0]),estado(b[1]),estado(b[2]));
    printf("---+---+---\n");
    printf(" %c | %c | %c\n",estado(b[3]),estado(b[4]),estado(b[5]));
    printf("---+---+---\n");
    printf(" %c | %c | %c\n",estado(b[6]),estado(b[7]),estado(b[8]));
}

int ganaste(const int tablero[9]) {
    
    unsigned gana[8][3] = {{0,1,2},{3,4,5},{6,7,8},{0,3,6},{1,4,7},{2,5,8},{0,4,8},{2,4,6}};
    int i;
    for(i = 0; i < 8; ++i) {
        if(tablero[gana[i][0]] != 0 &&
           tablero[gana[i][0]] == tablero[gana[i][1]] &&
           tablero[gana[i][0]] == tablero[gana[i][2]])
            return tablero[gana[i][2]];
    }
    return 0;
}

int minimax(int tablero[9], int jugador) {
    
// ¿Cómo es la posición del jugador (su turno) a bordo?
    int ganador = ganaste(tablero);
    if(ganador != 0) return ganador*jugador;

    int movimiento = -1;
    int puntuacion = -2; // Perder los movimientos son preferibles a ningún movimiento
    int i;
    for(i = 0; i < 9; ++i) {// Para todos los movimientos,
        if(tablero[i] == 0) {// Si es legal,
            tablero[i] = jugador;// Prueba el movimiento
            int thispuntuacion = -minimax(tablero, jugador*-1);
            if(thispuntuacion > puntuacion) {
                puntuacion = thispuntuacion;
                movimiento = i;
            }// Escoge el que es peor para el oponente
            tablero[i] = 0;// Restablecer el tablero después de probar
        }
    }
    if(movimiento == -1) return 0;
    return puntuacion;
}

void maquinamovimiento(int tablero[9]) {
    int movimiento = -1;
    int puntuacion = -2;
    int i;
    for(i = 0; i < 9; ++i) {
        if(tablero[i] == 0) {
            tablero[i] = 1;
            int temppuntuacion = -minimax(tablero, -1);
            tablero[i] = 0;
            if(temppuntuacion > puntuacion) {
                puntuacion = temppuntuacion;
                movimiento = i;
            }
        }
    }
    
// devuelve una puntuación basada en el árbol de minimax en un nodo determinado.
    tablero[movimiento] = 1;
}

void jugadormovimiento(int tablero[9]) {
int movimiento = 0;
do {
start:
printf("\nmovimiento ([0..8]): ");
scanf("%d", &movimiento);
if(tablero[movimiento] != 0) {
printf("Ya esta ocupado");
goto start;
}
printf("\n");
} while (movimiento >= 9 || movimiento < 0 && tablero[movimiento] == 0);
tablero[movimiento] = -1;
}

int TEST(int tablero[9], int jugador, int movimiento ){
if(tablero[9] > movimiento){
printf("cierto \n");}
else{
printf("falso \n"); }

if(tablero[9] >= movimiento){
for(int i=1; i=movimiento; i++){

if(tablero[9] > movimiento){
printf("cierto \n");}
else{

printf("ningun hijo cumple la condicion... \n");
      }
}
          }
}

int main() {
    int tablero[9] = {0,0,0,0,0,0,0,0,0};
// los cuadrados de la computadora son 1, los cuadrados del jugador son -1.
    printf("Maquina: O, Tu: X \noprima 1 para comenzar o 2 para que comienze primero la maquina \njugador (1) o jugador (2) ? ");
    int jugador=0;
    scanf("%d",&jugador);
    printf("\n");
    unsigned turn;
    for(turn = 0; turn < 9 && ganaste(tablero) == 0; ++turn) {
        if((turn+jugador) % 2 == 0)
            maquinamovimiento(tablero);
        else {
            dibujo(tablero);
            jugadormovimiento(tablero);
        }
    }
    switch(ganaste(tablero)) {
        case 0:
            printf("Empate\n");
            break;
        case 1:
            dibujo
(tablero);
            printf("Perdiste\n");
            break;
        case -1:
            printf("Ganaste!!!!!\n");
            break;
    }

}